The sketch of the parts is as follows:

 

 

 

 

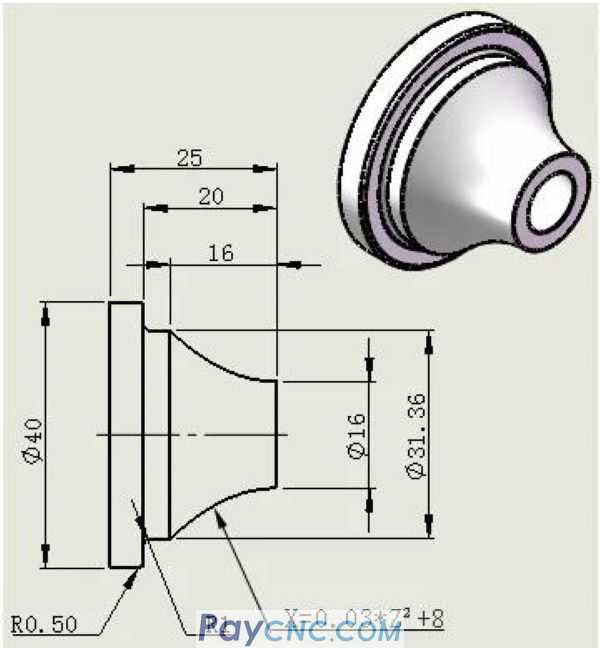
X=0.03*Z²+8 is the part curve equation.

 

From the perspective of the industry, there are many types of such products:

Such as parabola;

Such as ellipse;

Such as wavy lines;

Such as hyperbola;

Such as the Karman curve;

For example, the orthographic curve;

How to program the curve program?

 

You might think that this kind of part programming is "too complicated", and most of the parts you encounter in your work are regular parts. It's hard to think about it, so let's not learn it.

 

A person, always thinking from his own perspective, the road will become narrower and narrower!

 

A person who can always consider from more perspectives will become more and more awesome!

 

Today, Brother Jun will teach you a trick: Use mathematical equations to write NC macro programs, which will make you instantly NB.

 

This trick requires only two steps:

The first step: set variables into the equation

 

Step 2: Use equations to calculate coordinate points

 

How to apply these two steps? Just look at the example!

For example, the curve X=0.03*Z²+8 in the figure below

 

 

 

 

 

 

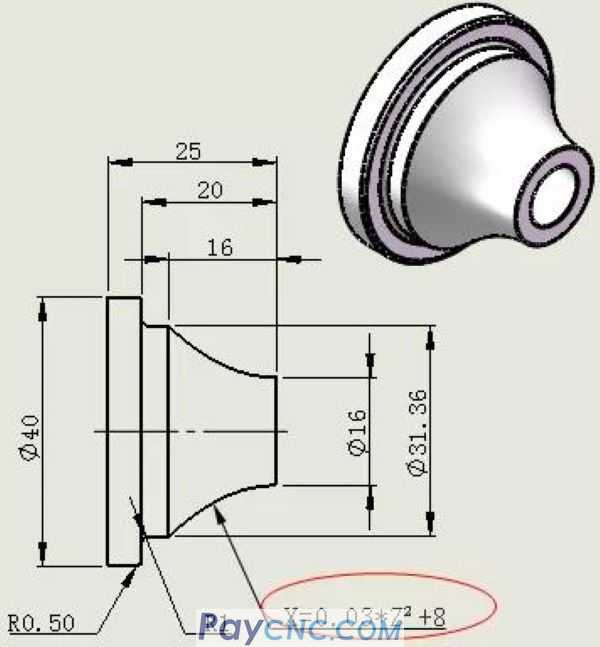
You may also think that I am not good at math, and the mathematical formulas don’t know what they mean, and some have not even heard of it.

 

Brother Jun emphasized again:

Knowing that a certain equation is not NB, only NB can be applied to the equation. If you can use the routine taught by Junge to use mathematical equations to write NC programs, it would be even more NB.

 

It is easy to know by carefully looking at the above parts diagram:

1. The value range of Z in this curve equation is from 0 to 16.

 

2. In this range (0~16), give Z a value, and there will be a corresponding X value. The value between X and Z satisfies this equation X=0.03*Z²+8

 

Well, the above two points are easy to understand.

 

The first step: set variables into the equation

It's very simple. For example, the variables of the Farak machine tool are composed of "#" and "numbers", such as #1, #2, #3 and so on.

 

Randomly specify two variables into the equation: X=0.03*Z²+8

Such as:

#1 represents Z.

#2 represents X.

 

Then the above equation is the following equation:

#2=0.03*#1*#1+8

 

Step 2: Use equations to calculate coordinate points

#2=0.03*#1*#1+8 is the equation of X=0.03*Z²+8.

#1 represents the value of the Z axis (curve).

#2 represents (curve) X-axis value.

 

among them:

1. The value range of #1 in the equation is from 0 to 16.

2. In this range (0~16), give #1 a value, and there will be a corresponding #2 value. The value between #1 and #2 satisfies this equation #2=0.03*#1*#1+8.

 

For example: #1=0, then the corresponding #2 value is equal to: 8

Because the value of #1 is substituted into the equation to calculate the value of #2.

 

Similarly, if:

#1=1, then #2=8.03

#1=2, then #2=8.12

#1=3, then #2=8.27

….

#1=16, then #2=15.68

 

Suppose, the more values ​​#2 takes, the more points there are, and then these points are connected by small line segments to form the curve of this equation. If these points are very dense, then the curve will be smoother with G01X#1Z#2 interpolation.

 

So how do you use equations to calculate coordinate points?

Answer: The increment operation of the variable.

 

The format of Falak's machine variable auto-increment operation is as follows:

#1=0

N1#2=0.03*#1*#1+8

……..Processing program

#1=#1+0.1

IF [#1LT16]GOTO1

 

The program runs sequentially from top to bottom, when it runs to the IF statement

 

Yes, if [#1LT16] jumps to the designated N1 block, and then runs the program from the N1 block to the next, namely:

Read the mathematical equation N1#2=0.03*#1*#1+8.

 

Read:...... CNC program.

 

Read variable #1=#1+0.1 auto-increment operation.

 

Read the IF [#2LT16] GOTO1 statement.

 

In this way, the values ​​of #1 and #2 are calculated through the increment operation of the variables.

 

 

Description:

The increment of the variable #1=#1+0.1, and the latter +0.1 means that the value of #1 will increase by 0.1 each time.

Of course, the latter value can also be given a small point, such as 0.01. The smaller the value, the more calculated data, which means that the denser the points, the smoother the interpolation curve will be.

 

With #1 and #2, then:

Add a program segment at a suitable position between IF and N1: G01X#2Z-#1, and the curve will be processed.

 

Where to add to?

 

As follows (position in red font):

...

#1=2

N1#2=0.03*#1*#1+8

G1X[2*#2]Z-#1F0.1 (converted to diameter programming, so 2*#2)

#1=#1+0.1

IF [#1LT16]GOTO1

….

First read the data of #1, #2, and then run G1X[2*#2]Z#1.

 

Well, the above program is organized as follows:

 

 

 

 

 

 

 

 

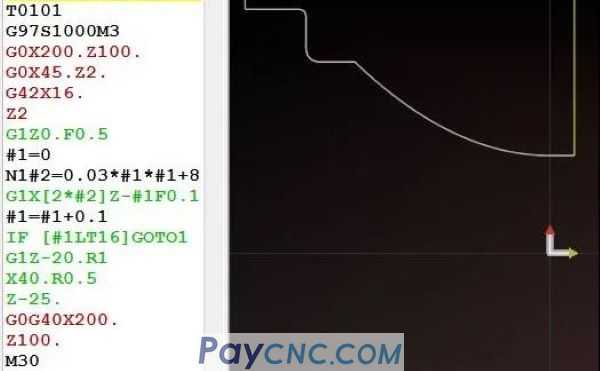
Soon, the programming of curve parts was completed.